3.1 A 2-fluid model applied to the environment
In the atmosphere, and in natural waters, gravitational forces
have a major effect on the fluid-dynamic phenomena, precisely
because of the fact that fragments of denser fluid (colder air or
more-saline water) are mingled with lighter ones.
The latter tend to rise, and the former to fall, often with striking effects.
For example, hurricanes gather their destructive power from the fact that the upwardly moving moist-air fragments, as they rise to lower-pressure altitudes, shed much of their water content as rain.
The latent heat of condensation has the effect of increasing still further the disparity of density between the upward- and downward-moving fluids, the relevant motion of which is therefore maintained, despite the friction between them.
Two-fluid models of turbulence are well able to simulate such phenomena. For example, the present author showed [57] how PHOENICS could be used to calculate the variation with time of the upward- and downward-moving members of the "atmospheric population" as a consequence of the heating and cooling of the surface of the earth.
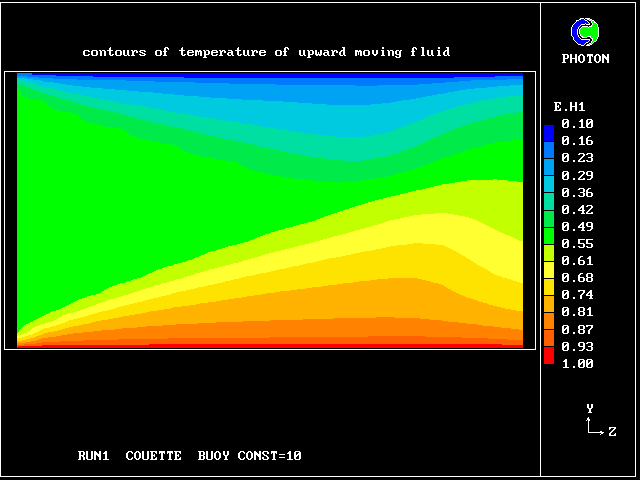
The following pictures represent what happens when a cool wind, moving from left to right, is heated as a consequence of contact with hot earth beneath it.

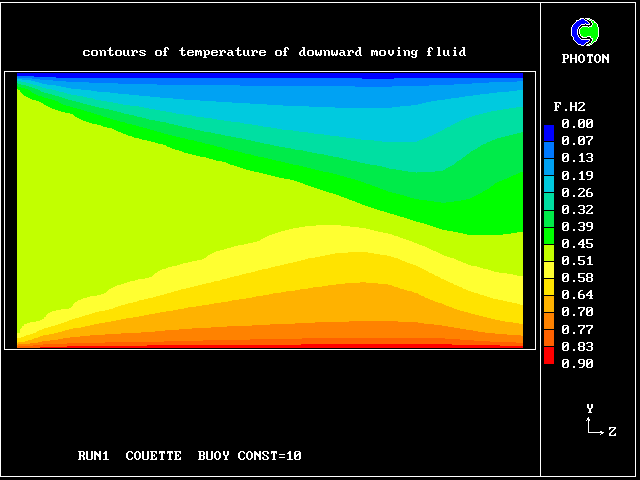
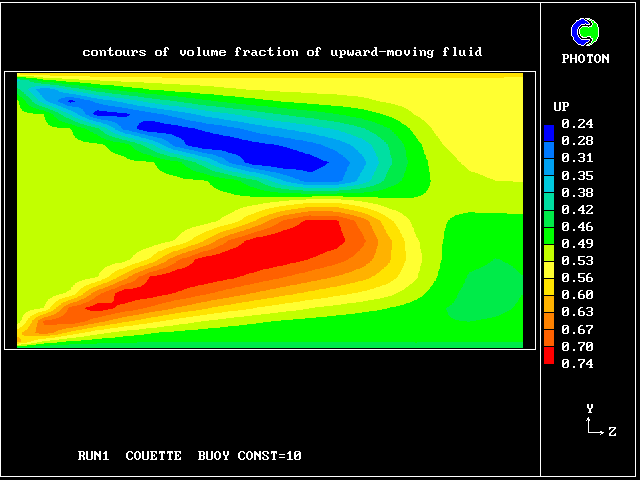
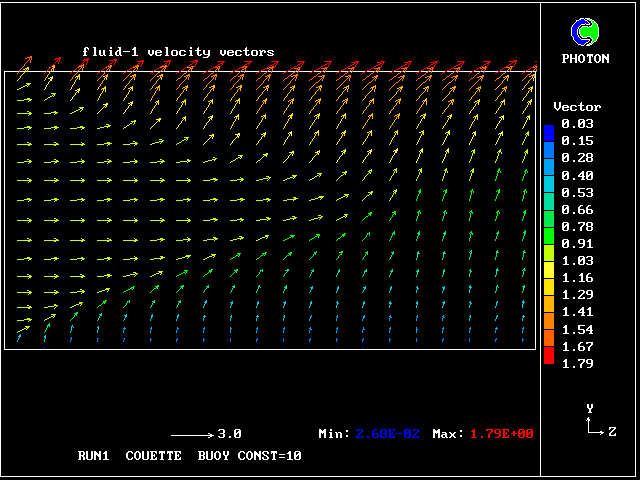
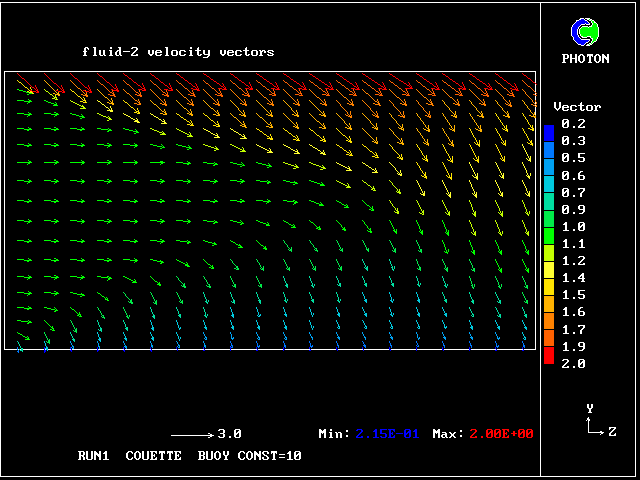
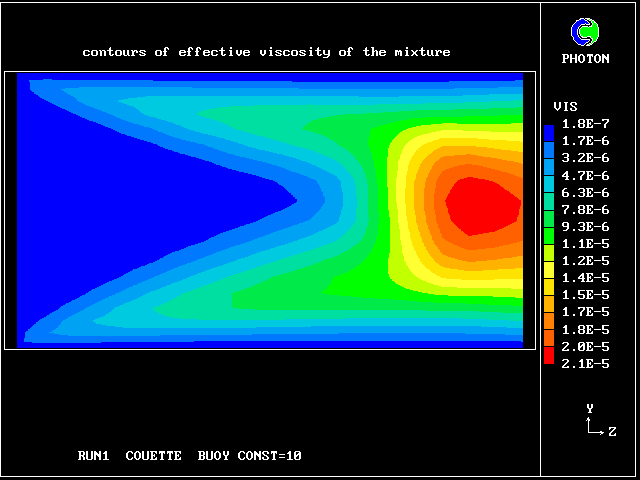
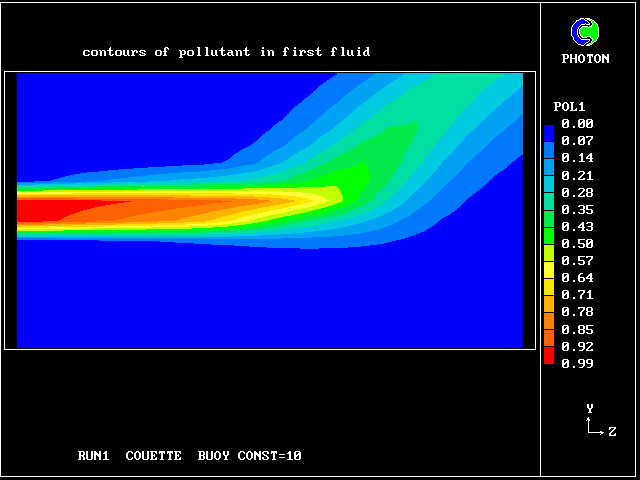
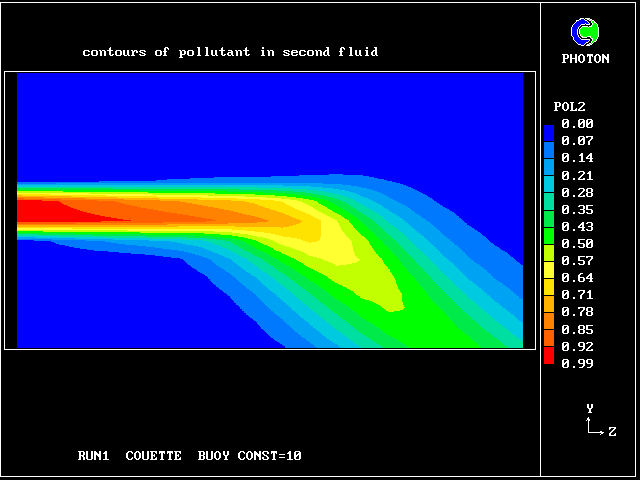
Some line-printer output from the PHOENICS library case W975 now follows; this concerns flow between a hot surface at rest and an upper cold moving surface. This is a Couette-flow idealization of an unstable atmosphere.
Each plot shows the variation with vertical distance of some properties of the two fluids, namely:
************************************************************
Fig.1 1 = V1 2 = V2 3 = W1 4 = W2
MINVAL= -1.871E-01 -1.871E-01 7.617E-13 7.617E-13
MAXVAL= 1.875E-01 1.875E-01 2.000E+00 2.000E+00
1.00 +....+....+....+...1+1..1+....+....+....+....+....4
+ 1 1 1 1 1 +
+ 11 1 1 1 1 1 443
+111 1 1 1 1 1 444 3+
1 4 4 4 4 4 4 4 4 4 4 331+
+ 444 4 4 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 33 2
224 3 3 3 3 3 3 3 2+
+4 333 2 2 2 2 2 222 +
433 2 2 2 2 2 2 +
+ 2 2 2 2 2 +
0.00 3....+....+....+....+...2+2..2+....+....+....+....+
0 non-dimensional vertical height 1.0
************************************************************
Fig.2 1 = H1 2 = H2
MINVAL= 0.000E+00 0.000E+00
MAXVAL= 1.000E+00 1.000E+00
1.00 1....+....+....+....+....+....+....+....+....+....+
+1 +
2 1 +
+2 111 1 +
+ 222 1 1 1 1 1 1 1 1 1 1 1 1 1 1 +
+ 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 111 +
+ 2 2 2 2 2 22 11+
+ 22 +
+ 21
+ +
0.00 +....+....+....+....+....+....+....+....+....+....2
0 non-dimensional vertical height 1.0
************************************************************
Fig.3 1 = UP 2 = MDOT
MINVAL= 0.000E+00 -2.038E-02
MAXVAL= 1.000E+00 1.992E-02
1.00 2....+....+....+....+....+....+....+....+....+....+
+ +
+ +
+2 +
+ 2222 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 111111
+ 2 2 +
111111 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2222 +
+ 2+
+ +
+ +
0.00 +....+....+....+....+....+....+....+....+....+....2
0 non-dimensional vertical height 1.0
************************************************************
Despite the crudeness of the graphical representation, information
of physical interest can be derived. Thus, one may see from Fig.1
that the upward-rising fluid has the smaller horizontal velocity,
for the understandable reason that it comes from a lower-velocity
region.
Fig. 2 reveals that it is hotter than the downward-moving fluid, no doubt because it has received heat from the warmer regions, closer to the ground.
Fig. 3 shows that, according to this model, the volume fractions of the two fluids are not uniform. Thus there is more upward-moving fluid in the upper half (ie the right-hand half on the diagram) of the layer than in the lower. It is the inter-fluid mass-transfer rate (MDOT) which maintains the balance.
Before leaving this topic, it is worth remarking, to those to whom the two-fluid model is new, that this Couette-flow study can be regarded as a refinement of the idea which Ludwig Prandtl presented seventy years ago as the "mixing-length model". Prandtl had to make assumptions, where the two-model permits calculations. Thus, Prandtl had to assume that the differences of the vertical velocity were equal to the differences of the horizontal velocity, and that the volume fractions of the two fluids were equal.
As mentioned above, the two-fluid concept was inherent in the thinking of both Reynolds and Prandtl. To develop it further is to continue a distinguished tradition.